FFT Zero-Padding Strategies - Computing Transform Length
For 1-D applications with very long vectors, the time required to compute the transform size could be significant.
Speed of repeated division method
In my previous post in this series, I described a method for choosing the FFT transform length when computing a full convolution. The method is based on the idea of choosing a length whose prime factors are no greater than 7.
To find such a length, I wrote some code that used repeated division to determine whether $N$ has factors greater than 7. The code would then simply increment $N$ until it found a suitable length.
function Np = fftTransformLength_repeated_division(N)
Np = N;
while true
% Divide n evenly, as many times as possible, by the factors 2, 3,
% 5, and 7.
r = Np;
for p = [2 3 5 7]
while (r > 1) && (mod(r, p) == 0)
r = r / p;
end
end
if r == 1
break
else
Np = Np + 1;
end
end
end
Because I was interested in 2-D applications with relatively small transform sizes (in the thousands), I didn't think too much about the efficiency of this function. For 1-D applications with very long vectors, though, the time required to compute the transform size could be significant. For example, $N=8505001$ is prime, and the nearest larger integer with prime factors no larger than 7 is $N_p =8573040$ , which is 68039 integers away. Let's see how much time that would take.
N = 8505001;
Np = fftTransformLength_repeated_division(N)
Np = 8573040
f = @() fftTransformLength_repeated_division(N);
timeit(f)
ans = 0.0322
Is 32 milliseconds a long time?
It is. It's about a third of the time required for the corresponding FFT computation:
x = rand(1,N);
g = @() fft(x,Np);
timeit(g)
ans = 0.0946
Alternative computation methods
I'd like to thank Chris Turnes (MATLAB Math team developer at MathWorks; fellow Georgia Tech grad) and Cris Luengo (principal data scientist at Deepcell; creator of DIPlib) for sharing their thoughts with me about alternative computation methods. Chris taught me how to construct a lookup table containing all integers (up to a specified maximum value) whose prime factors are no larger than 7. He suggested that such a table would have only a modest size, even for very large maximum transform sizes. Cris pointed out that OpenCV uses the lookup table approach with a binary search and that PocketFFT uses only multiplications and divisions by 2. Chris and Cris both did experiments that suggest there is value in using these other methods.
Constructing the lookup table
Here is a function that lists all the integers, up to some maximum value, whose prime factors are no greater than 7. The implementation concept here is from Chris Turnes.
function P = generateLookupTable(N)
P = 2.^(0:ceil(log2(N)));
P = P(:) * 3.^(0:ceil(log(N)/log(3)));
P = P(:) * 5.^(0:ceil(log(N)/log(5)));
P = P(:) * 7.^(0:ceil(log(N)/log(7)));
% Sort and trim P so that it contains only values up to N. Add 0 to the
% set of values.
P = sort(P(:));
i = find(P >= N, 1, "first");
P = [0 ; P(1:i)];
end
Let's find all of the desirable transform lengths up to approximately a billion.
P = generateLookupTable(2^30);
size(P)
ans = 1x2
5261 1
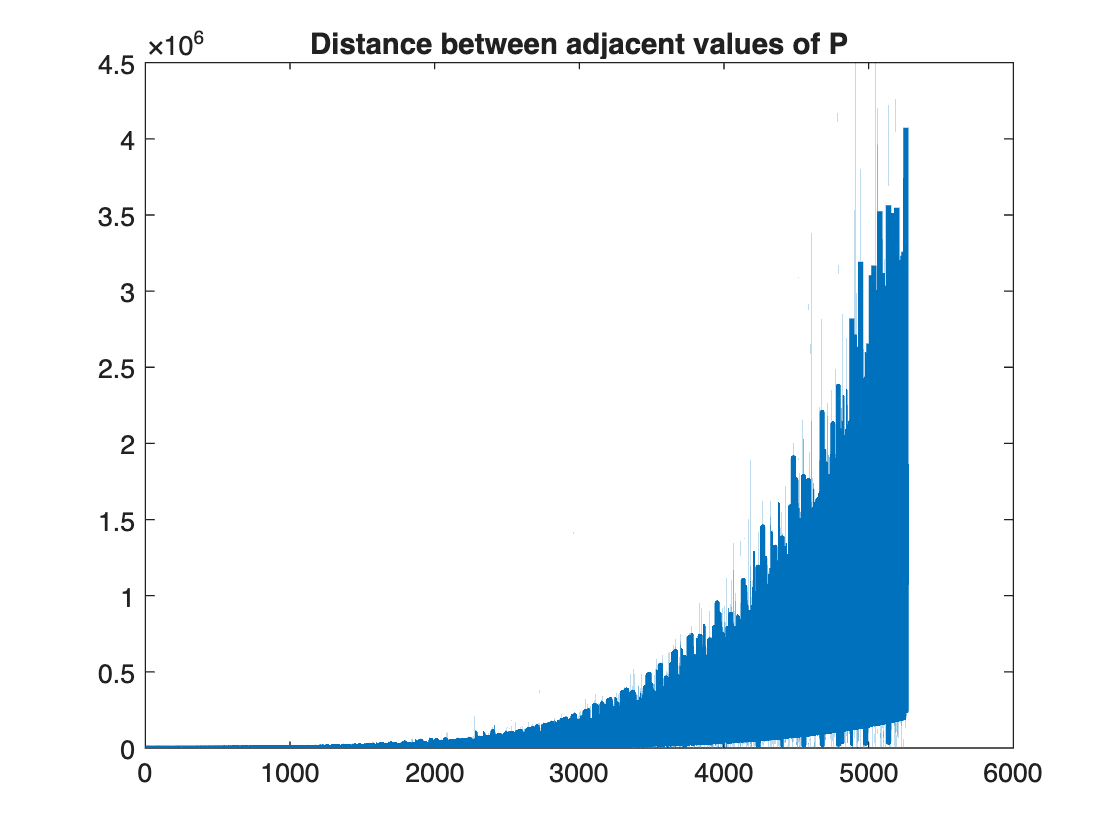
How are those values spread out?
plot(diff(P))
title("Distance between adjacent values of P")
Performance of the lookup-table method
Now let's try using a simple search of P to implement an alternative method to find a good transform length.
function Np = fftTransformLength_lookup_table(N,P)
Np = P(find(P >= N, 1, "first"));
end
How long does this take for the example above, $N=8505001$ ?
N = 8505001;
P = generateLookupTable(1e9);
h = @() fftTransformLength_lookup_table(N,P);
timeit(h)
ans = 7.1154e-06
Further optimizations could be explored, but already it takes only a few microseconds, about 4,500 times faster than the repeated division method for this particular case.
Let's check performance for a large power of two, which I would expect to be a much better case for the repeated division method.
N = 2^30;
timeit(@() fftTransformLength_repeated_division(N))
Warning: The measured time for F may be inaccurate because it is running too fast. Try measuring something that takes longer.
ans = 0
timeit(@() fftTransformLength_lookup_table(N,P))
ans = 7.4774e-06
The repeated division method is so fast, in this case, that the time required is not measurable.
However, I am inclined to always use the lookup table method, and I have updated my fftTransformLength function (GitHub link, File Exchange link) to do that.
MathWorks enhancement request: Add an FFT transform length function
I have submitted an enhancement request to MathWorks to add a function for computing good FFT transform lengths, as described in this series.

